Curiousily

Predicting House Prices

11.10.2016 — R, Regression, Random Forest — 3 min read

So you have a house for sale or buying one? What is a fair price for it? Can we predict it correctly?

Let’s use the “House Sales in King County” data available at Kaggle to answer that question. Each row of the dataset contains information about a home sold between May 2014 and May 2015 along with the price in US dollars. Some of the other features include:

bedrooms - number of bedrooms
bathrooms - number of bathrooms
floors - number of floors
yr_built - year built
zipcode
long - longitude
lat - latitude
condition - building condition (ordered categorical variable in the range 1 - 5)
grade - construction quality of improvements (ordered categorical variable in the range 1 - 13)

If not interested in house prices you still can learn something about regression, classification trees, and extreme gradient boosting.

Fire up R and load some libraries

1library(ggplot2)
2library(reshape2)
3library(plyr)
4library(dplyr)
5library(rpart)
6library(rpart.plot)
7library(caret)
8library(doMC)
9library(scales)
10library(GGally)

Load our utility functions, make results reproducible and instruct R to use all our CPU cores (my PC has 8 cores, you might want to revise that value for yours).

1source("utils.R")
2
3set.seed(42)
4theme_set(theme_minimal())
5registerDoMC(cores = 8)
6options(warn=-1)

Load and preprocess the dataset

1df <- read.csv("data/kc_house_data.csv", stringsAsFactors = FALSE)

1print(paste("rows:", nrow(df), "cols:", ncol(df)))

1[1] "rows: 21613 cols: 21"

Remove id and date columns and instruct R to interpret condition, view, grade and waterfront as factors.

1df <- df[-c(1, 2)]
2df$condition <- as.factor(df$condition)
3df$view <- as.factor(df$view)
4df$grade <- as.factor(df$grade)
5df$waterfront <- as.factor(df$waterfront)

Exploration

Do we have missing data?

1ggplot_missing(df)

{:.center}

It looks like everything is in here! Great!

Maps

The following awesome maps were created by Thierry Ellena. Let’s have a look at them:

House locations
Number of houses by zipcode
Price by zipcode

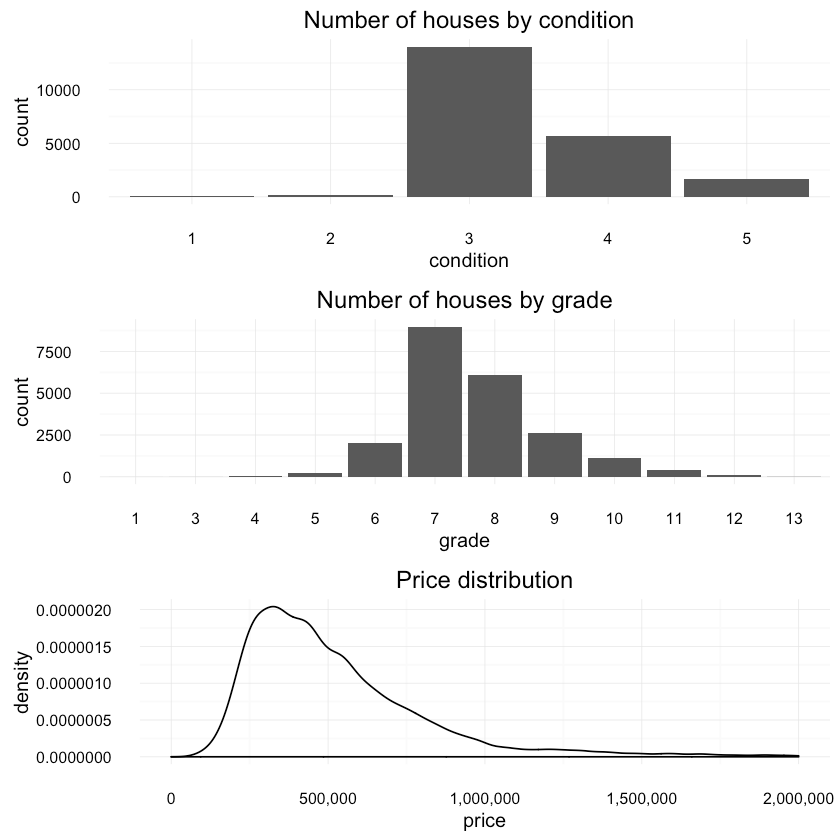
Let’s look at the distribution of house condtion, grade and price:

1p1 <- qplot(condition, data=df, geom = "bar",
2    main="Number of houses by condition")
3
4p2 <- qplot(grade, data=df, geom = "bar",
5    main="Number of houses by grade")
6
7p3 <- ggplot(df, aes(price)) + geom_density() +
8    scale_y_continuous(labels = comma) +
9    scale_x_continuous(labels = comma, limits = c(0, 2e+06)) +
10    xlab("price") +
11    ggtitle("Price distribution")
12
13multiplot(p1, p2, p3)

{:.center}

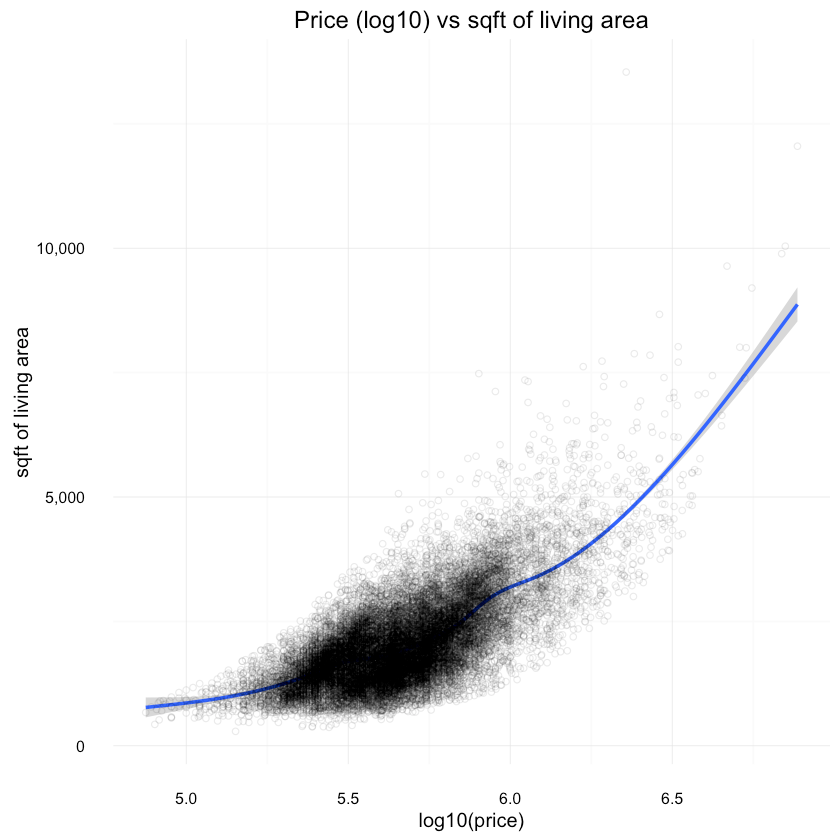
And a look at price (log10) vs other features:

1ggplot(df, aes(x=log10(price), y=sqft_living)) +
2    geom_smooth() +
3    scale_y_continuous(labels = comma) +
4    scale_x_continuous(labels = comma) +
5    ylab("sqft of living area") +
6    geom_point(shape=1, alpha=1/10) +
7    ggtitle("Price (log10) vs sqft of living area")

{:.center}

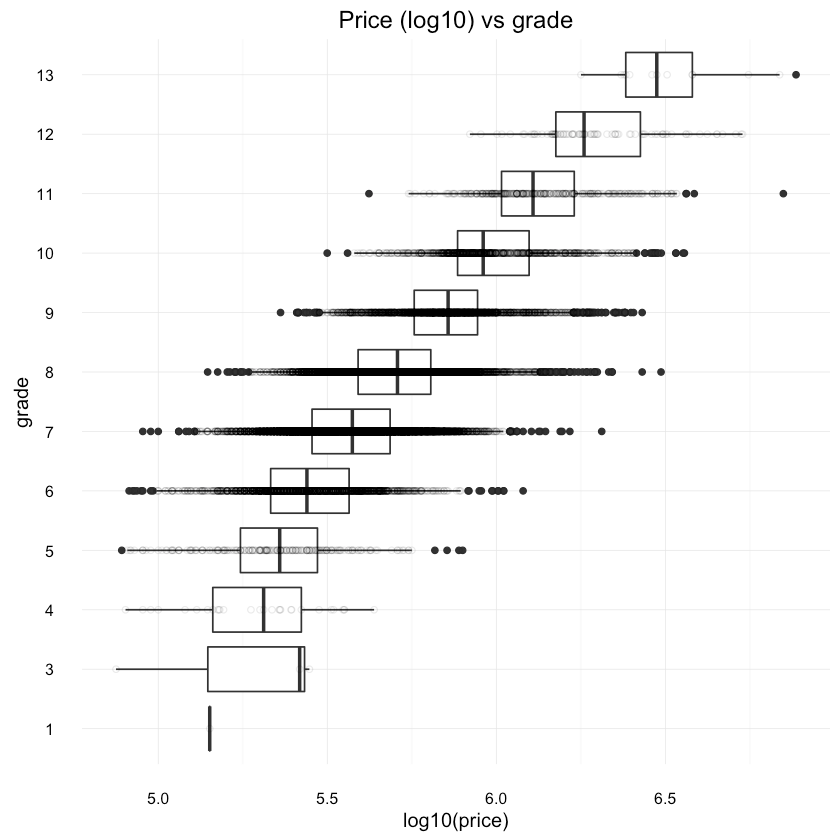
1ggplot(df, aes(x=grade, y=log10(price))) +
2    geom_boxplot() +
3    scale_y_continuous(labels = comma) +
4    coord_flip() +
5    geom_point(shape=1, alpha=1/10) +
6    ggtitle("Price (log10) vs grade")

{:.center}

1ggplot(df, aes(x=condition, y=log10(price))) +
2    geom_boxplot() +
3    scale_y_continuous(labels = comma) +
4    coord_flip() +
5    geom_point(shape=1, alpha=1/10) +
6    ggtitle("Price (log10) vs condition")

{:.center}

1ggplot(df, aes(x=as.factor(floors), y=log10(price))) +
2    geom_boxplot() +
3    scale_y_continuous(labels = comma) +
4    xlab("floors") +
5    coord_flip() +
6    geom_point(shape=1, alpha=1/10) +
7    ggtitle("Price (log10) vs number of floors")

{:.center}

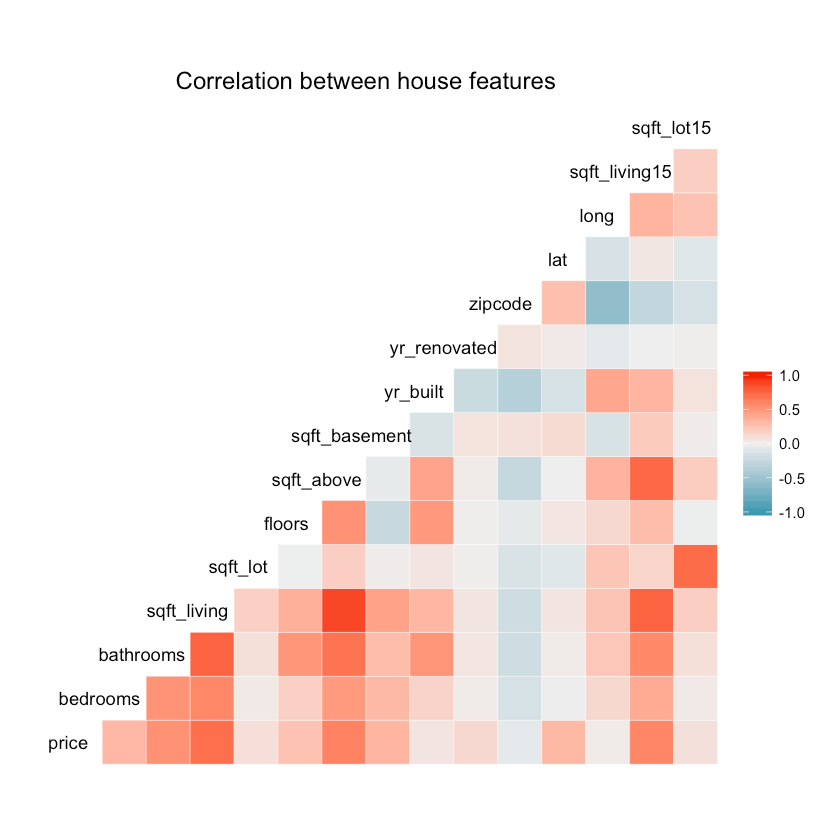
How different features correlate?

1ggcorr(df, hjust = 0.8, layout.exp = 1) +
2    ggtitle("Correlation between house features")

{:.center}

Splitting the data

We will split the data using the caret package. 90% will be used for training and 10% for testing.

1train_idx = createDataPartition(df$price, p=.9, list=FALSE)
2
3train <- df[train_idx, ]
4test <- df[-train_idx, ]

We will extract the labels (true values) from our test dataset.

1test_labels <- test[, 1]

First attempt of building a model

Let’s build a decision tree with the rpart package using all features (except price) as predictors:

1tree_fit <- rpart(price ~ ., data=df)
2tree_predicted <- predict(tree_fit, test)

And the results of our model:

1summary(tree_predicted)

1Min. 1st Qu.  Median    Mean 3rd Qu.    Max.
2 315400  315400  462800  542000  654900 5081000

1summary(test_labels)

1Min. 1st Qu.  Median    Mean 3rd Qu.    Max.
2  82000  322100  450000  536300  643900 3419000

1cor(tree_predicted, test_labels)

0.814574873081786

1rmse(tree_predicted, test_labels)

197634.31260839

How the actual and predicted distributions compare to each other?

1res <- data.frame(price=c(tree_predicted, test_labels),
2          type=c(replicate(length(tree_predicted), "predicted"),
3                 replicate(length(test_labels), "actual")))
4
5ggplot(res, aes(x=price, colour=type)) +
6    scale_x_continuous(labels = comma, limits = c(0, 2e+06)) +
7    scale_y_continuous(labels = comma) +
8    geom_density()

{:.center}

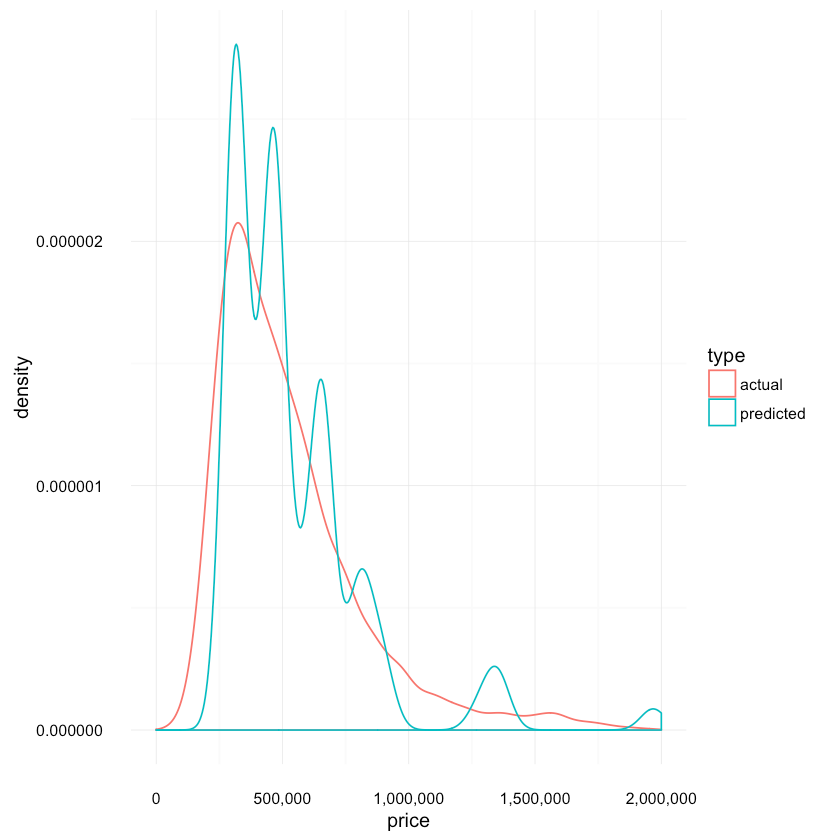
Not very good, eh? Let’s dig a bit deeper.

How does our model looks like?

1rpart.plot(tree_fit, digits = 4, fallen.leaves = TRUE,
2             type = 3, extra = 101)

{:.center}

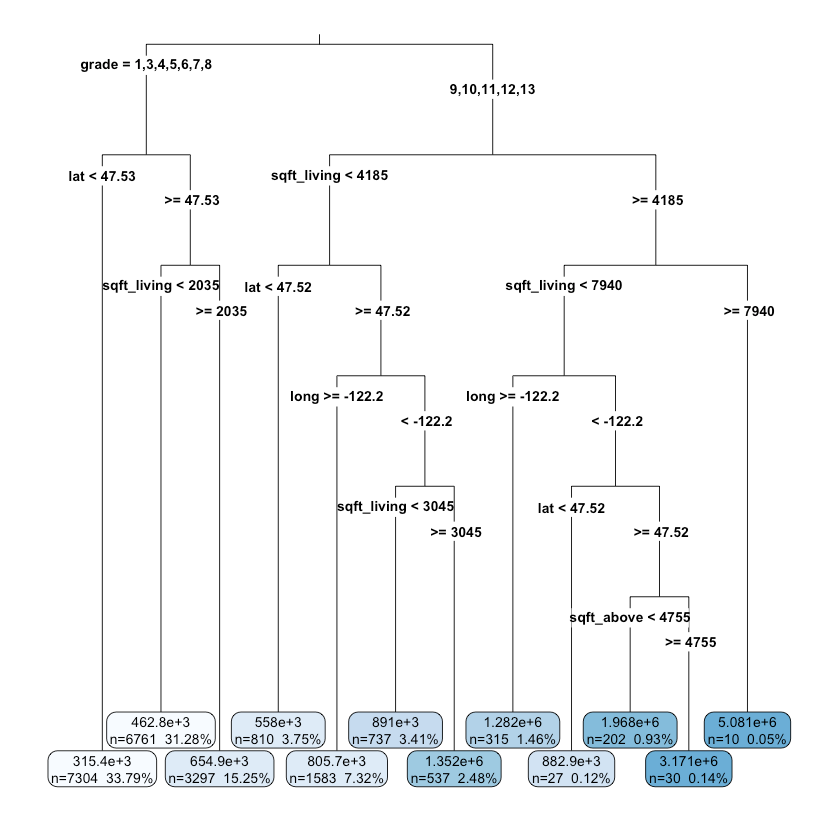
It seems that the grade, location (lat, long), square feet are important factors for deciding the price of a house.

Fitting a xgbTree model

That was a good first attempt. Ok, it wasn’t even good. So, can we do better? Let’s try an ensemble of boosted trees. For good intro to boosted trees see: Introduction to Boosted Trees.

First, we will set up the resampling method used by caret. 10 cross-validation passes should do (preferably in parallel).

1ctrl = trainControl(method="cv", number=10, allowParallel = TRUE)

Our next step is to find good parameters for XGBoost. See the references below to find out how to tune the parameters for your particular problem. Those are the parameters I’ve tried:

1param_grid <-  expand.grid(eta = c(0.3, 0.5, 0.8),
2                        max_depth = c(4:10),
3                        gamma = c(0),
4                        colsample_bytree = c(0.5, 0.6, 0.7),
5                        nrounds = c(120, 140, 150, 170),
6                        min_child_weight = c(1))

After trying them out, the following were chosen:

1param_grid <- expand.grid(eta=c(0.3),
2                          max_depth= c(6),
3                          gamma = c(0),
4                          colsample_bytree = c(0.6),
5                          nrounds = c(120),
6                          min_child_weight = c(1))

Finally, time to train our model using root mean squared error as score metric:

1xgb_fit = train(price ~ .,
2            data=df, method="xgbTree", metric="RMSE",
3            trControl=ctrl, subset = train_idx, tuneGrid=param_grid)
4
5xgb_predicted = predict(xgb_fit, test, "raw")

and the results:

1summary(xgb_predicted)

1Min. 1st Qu.  Median    Mean 3rd Qu.    Max.
2 143100  323700  464700  542100  649700 6076000

1summary(test_labels)

1Min. 1st Qu.  Median    Mean 3rd Qu.    Max.
2  82000  322100  450000  536300  643900 3419000

1cor(xgb_predicted, test_labels)

0.926845603997267

1rmse(xgb_predicted, test_labels)

132324.026367212

comparison of actual and predicted distributions:

1res <- data.frame(price=c(xgb_predicted, test_labels),
2            type=c(replicate(length(xgb_predicted), "predicted"),
3                  replicate(length(test_labels), "actual")))
4
5ggplot(res, aes(x=price, colour=type)) +
6    scale_x_continuous(labels = comma, limits = c(0, 2e+06)) +
7    scale_y_continuous(labels = comma) +
8    geom_density()

{:.center}

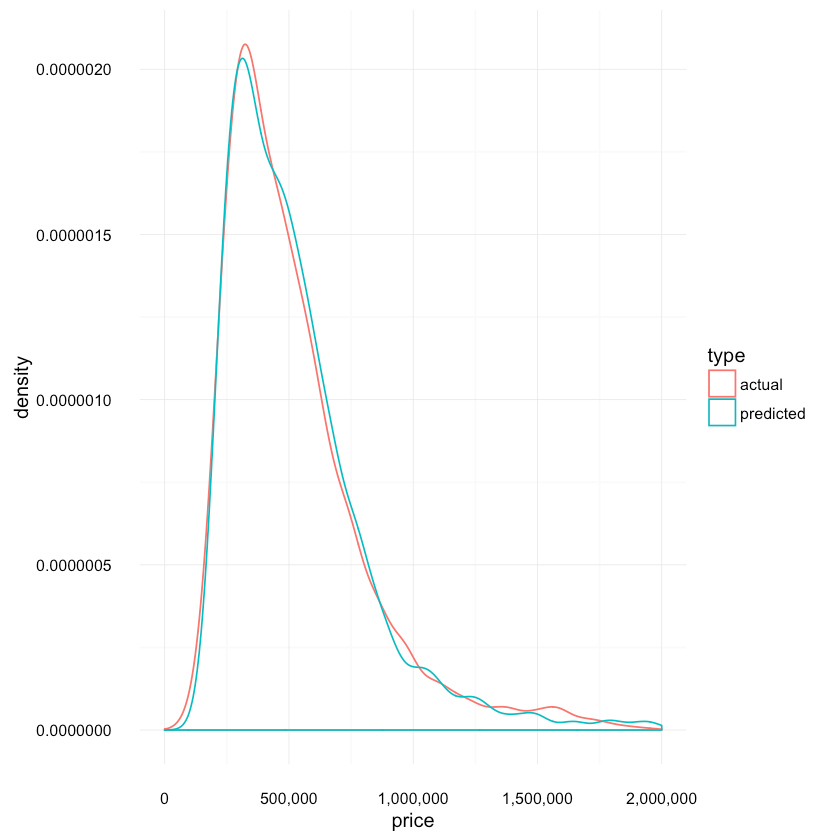
The distributions look much more similar compared to the one produced by the decision tree model.

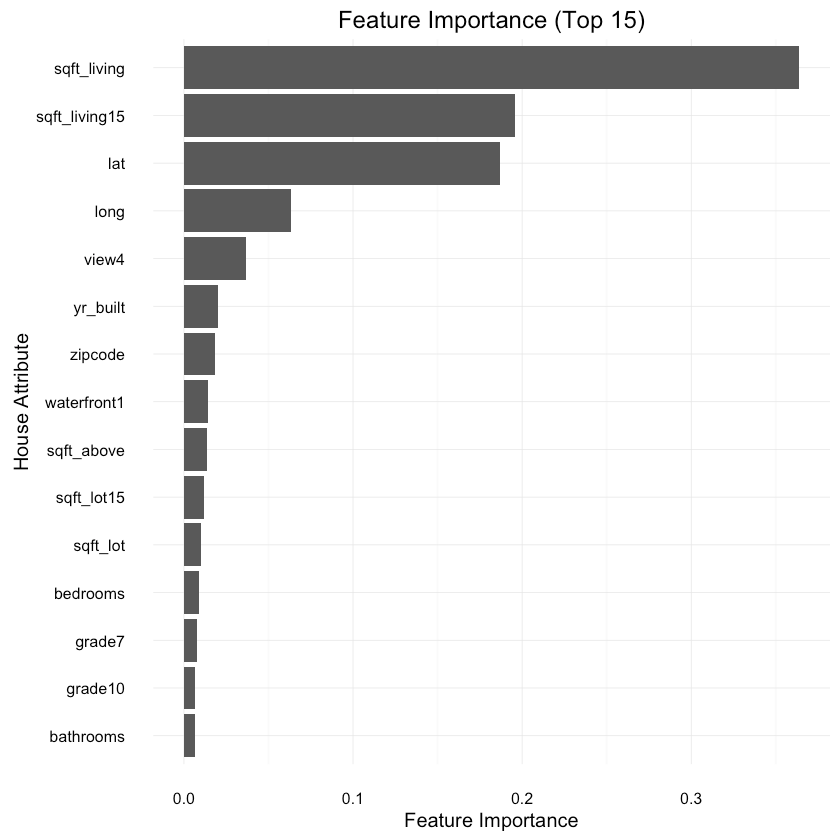
What are the most important features according to our model?

1imp <- varImp(xgb_fit, scale = FALSE)
2
3imp_names = rev(rownames(imp$importance))
4imp_vals = rev(imp$importance[, 1])
5
6var_importance <- data_frame(variable=imp_names,
7                             importance=imp_vals)
8var_importance <- arrange(var_importance, importance)
9var_importance$variable <- factor(var_importance$variable,
10        levels=var_importance$variable)
11
12var_importance_top_15 = var_importance[with(var_importance,
13        order(-importance)), ][1:15, ]
14
15ggplot(var_importance_top_15, aes(x=variable, weight=importance)) +
16 geom_bar(position="dodge") + ggtitle("Feature Importance (Top 15)") +
17 coord_flip() + xlab("House Attribute") + ylab("Feature Importance") +
18 theme(legend.position="none")

{:.center}

Compare distributions of predictions

Let’s see how the tree distributions compare to each other:

1res <- data.frame(price=c(tree_predicted, xgb_predicted, test_labels),
2                  type=c(replicate(length(tree_predicted), "tree"),
3                         replicate(length(xgb_predicted), "xgb"),
4                         replicate(length(test_labels), "actual")
5                        ))
6
7ggplot(res, aes(x=price, colour=type)) +
8    scale_x_continuous(labels = comma, limits = c(0,2e+06)) +
9    scale_y_continuous(labels = comma) +
10    geom_density()

{:.center}

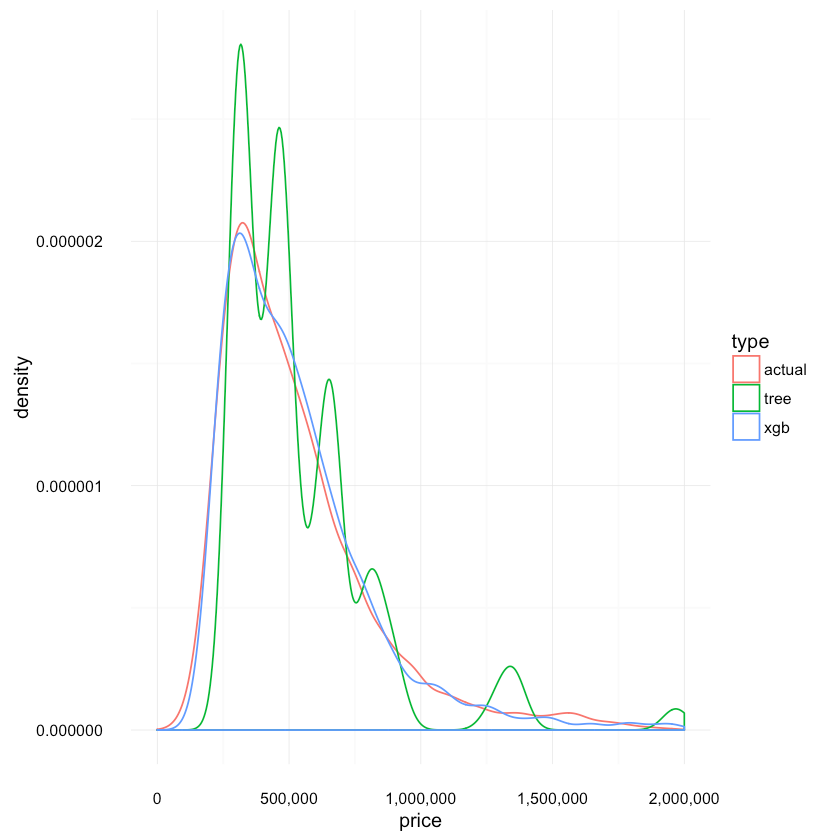
Again, we can confirm that the Boosted Trees model provides much more accurate distribution with its predictions.

How well we did, really?

Let’s randomly choose 10 rows and look at the difference between predicted and actual price:

1test_sample <- sample_n(test, 10, replace=FALSE)
2test_predictions <- predict(xgb_fit, test_sample, "raw")
3actual_prices <- round(test_sample$price, 0)
4predicted_prices <- round(test_predictions, 0)
5data.frame(actual=actual_prices,
6    predicted=predicted_prices,
7    difference=actual_prices-predicted_prices)

actual	predicted	difference
680000	566726	113274
1400000	1502961	-102961
400000	465854	-65854
468000	382870	85130
220000	208510	11490
525000	553434	-28434
404000	559599	-155599
327000	316226	10774
475000	460288	14712
443000	431310	11690

Is this good? Well, personally I expected more. However, there are certainly more things to try if you are up to it. One interesting question that arises after receiving prediction is: How sure the model is that the price is what he tells us it is? But that is a topic for another post.

References

RMSE explained
Gradient Boosting explained
Dataset attributes explained
More information for the attributes

XGBoost

Introduction to XGBoost
Optimizing XGBoost
Parameter tuning in XGBoost

caret

Tuning parameters in caret

Want to be a Machine Learning expert?

Join the weekly newsletter on Data Science, Deep Learning and Machine Learning in your inbox, curated by me! Chosen by 10,000+ Machine Learning practitioners. (There might be some exclusive content, too!)

You'll never get spam from me

Hacker's Guide to Neural Networks in JavaScript

Build Machine Learning models (especially Deep Neural Networks) that you can easily integrate with existing or new web apps. Think of your ReactJs, Vue, or Angular app enhanced with the power of Machine Learning models.

Get SH*T Done with PyTorch

Learn how to solve real-world problems with Deep Learning models (NLP, Computer Vision, and Time Series). Go from prototyping to deployment with PyTorch and Python!

Hacker's Guide to Machine Learning with Python

This book brings the fundamentals of Machine Learning to you, using tools and techniques used to solve real-world problems in Computer Vision, Natural Language Processing, and Time Series analysis. The skills taught in this book will lay the foundation for you to advance your journey to Machine Learning Mastery!

Hands-On Machine Learning from Scratch

This book will guide you on your journey to deeper Machine Learning understanding by developing algorithms in Python from scratch! Learn why and when Machine learning is the right tool for the job and how to improve low performing models!