Curiousily

Predicting the next Fibonacci number with Linear Regression in TensorFlow.js - Machine Learning in the Browser for Hackers (Part 1)

20.06.2018 — Machine Learning, JavaScript, TensorFlow, Neural Network — 7 min read

Welcome to the first (or 0th) part of the series! Together we will explore the limits of what is possible (and probably impossible) with the current state of using JavaScript for Machine Learning in the browser!

The complete source code can be found on GitHub if you want to follow along. Additionally, I’ve included a gist showing the complete JavaScript code at the end of the post. Here is a link to a Live Demo, you must open your browser console to see the results.

What are we trying to do?

Given some random number $x$ that belongs to the Fibonacci sequence, we’re going to predict the next one.

If you don’t know what a Fibonacci number is (shame on you!) you can take a look here. The Fibonacci numbers are all-powerful, some say that they even have magical powers (even though they don’t contain the number that is the answer to the ultimate question of life, the universe, and everything).

Simply put, the next Fibonacci number is generated by summing the previous two (after the first two). Here are the first couple of numbers:

$1, 1, 2, 3, 5, 8, 13, 21 \ldots$

Can we build a model using TensorFlow.js that predicts the next Fibonacci number?

What is Linear Regression?

Simple Linear Regression is one of the most basic models you can try out. This model operates under the assumption that there is a linear relationship between a variable $Y$ and an independent variable $X$ . Here’s the equation that describes the model:

Y = aX + b

What $a$ - “slope” and $b$ - “intercept” are parameters for our model. And TensorFlow.js is going to help us find their values. That is, find values that best describe our data. Want to see what the process looks like? Here is a picture:

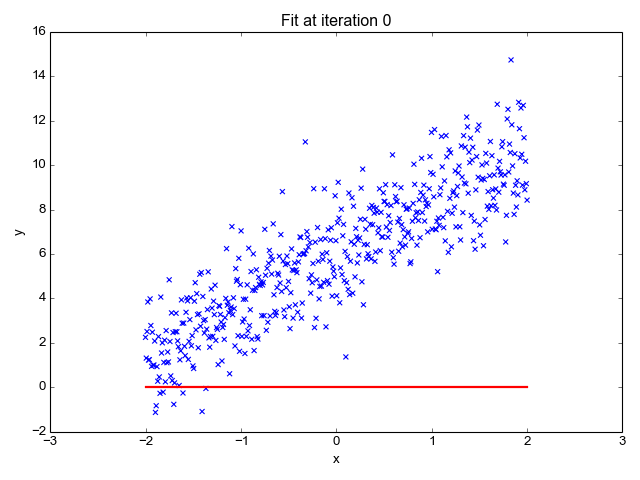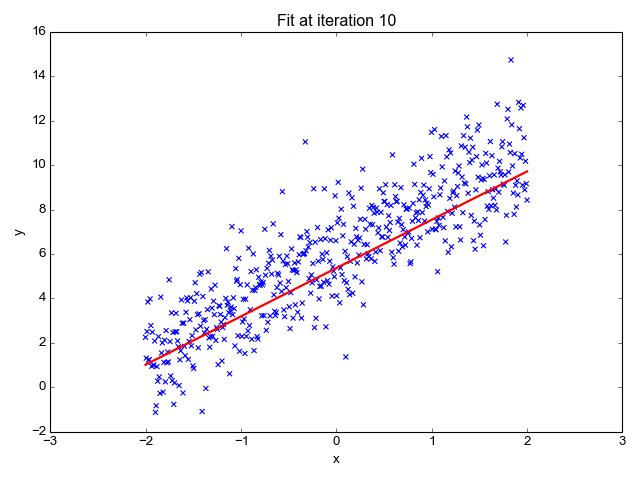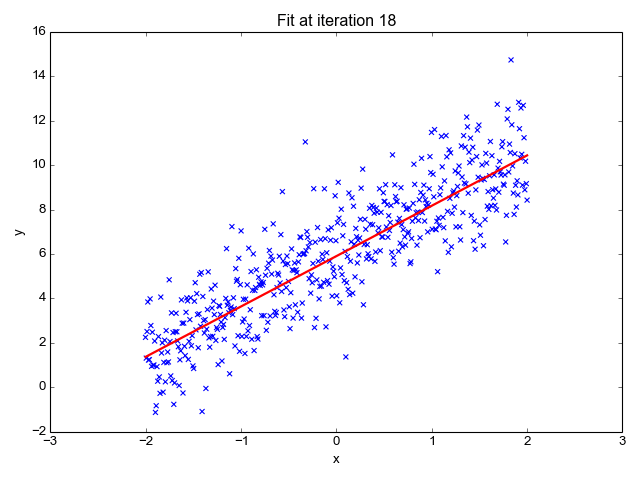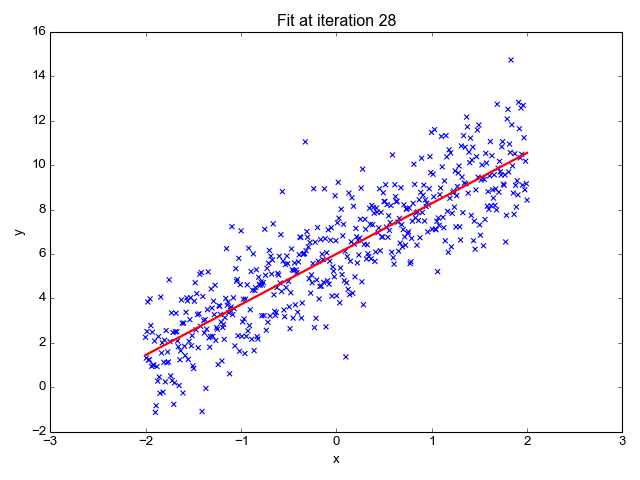source: https://towardsdatascience.com

What you’re observing is the process of fitting the straight line through an example dataset. You can see that the line (that is, the model) starts at some crappy position and after some training (indicated by the increasing number of iterations) it is right in the middle of our data. Note that there are points that are far away from our line. Is this an issue? That’s a topic for another discussion.

But what is Linear Regression? We only learned about Simple Linear Regression so far. Linear Regression (or Multiple Linear Regression) has two or more independent variables (think $X$ s). That’s all folks!

Okay, we have a plan now, we will create a Linear Regression model that can predict the next Fibonacci number. For that, we’re going to need a powerful tool.

What is TensorFlow.js

A JavaScript library for training and deploying ML models in the browser and on Node.js

TensorFlow.js makes it super easy to get started with Machine Learning. But why?

No need to know any of the fancy pantsy languages like C++, Python or Java, just JavaScript. But hey you probably know some already!
Do you know where you can run JavaScript? That’s right pretty much everywhere - phones, tablets, PCs, Macs and your grandma bike (just checking if you’re still with me). The best part is that you don’t need to install anything - simply include a JavaScript file. And yes, you guessed it, that means you can train your models on Android and iOS phones too (PyTorch I am looking at you)!

Installing TensorFlow.js

Installing TensorFlow.js is simple. Being a JavaScript library, we have to include it in the <head> tag of an HTML page. Open up your favorite text editor (as long it is VIM) and create the following HTML file:

1<!DOCTYPE html>
2<html>
3  <head>
4    <script src="https://cdn.jsdelivr.net/npm/@tensorflow/tfjs@0.11.6"></script>
5    <script src="index.js"></script>
6  </head>
7
8  <body></body>
9</html>

At the time of this writing, the most recent version of TensorFlow.js is 0.11.6. If a newer version is available, when you read these lines, you should consider updating it and fiddling with it if nothing works.

All of our JavaScript is going to be written in index.js. Now might be a good time to create it.

What is a Tensor?

Tensors are just multidimensional arrays of numbers. They’re the main building block you’re going to use when building models in TensorFlow (still wondering about the name of the library?). When performing operations, on them, you get new Tensors (that is, they are immutable). Creating a Tensor is easy:

1const myFirstTensor = tf.scalar(42)

Let’s try to print the value of our Tensor:

1console.log(myFirstTensor)

1e {isDisposedInternal: false, size: 1, shape: Array(0), dtype: "float32", strides: Array(0), …}

Uh, what the crap is that? Welcome to the world of TensorFlow, where everything is just a bit off. It wouldn’t be fun if console.log() was working as expected, would it?

Ok, here is the solution to our problem:

1myFirstTensor.print()

1Tensor
2    42

And now you know the most well-kept secret of TensorFlow - how to print some values.

Here is how we can create a vector (1d Tensor):

1const oneDimTensor = tf.tensor1d([1, 2, 3])

Let’s practice our printing superpowers:

1oneDimTensor.print()

1Tensor
2    [1, 2, 3]

Depending on your needs you can use other helper functions to create Tensors: tf.tensor2d(), tf.tensor3d() and tf.tensor4d().

Predicting the next Fibonacci number

Now that we know what Tensors are we can start building our model. First up - creating the training data.

Preparing the training data

Remember, our job is to find the values of the parameters $a$ and $b$ . Thankfully, we won’t have to do this by hand - TensorFlow.js can help us! To do that, we need training data, preferably lots of it. Our model is going to use that data find good values for $a$ and $b$ . In our case, “good values” are values that best predict the next Fibonacci number.

Ok, how to create the data? Fortunately, the sequence of Fibonacci numbers $F_n$ can be generated using the following recurrence:

F_n = F_{n - 1} + F_{n - 2}

We can use that to create an iterative version (why not recursive?) in JavaScript that generates it:

1function fibonacci(num) {
2  var a = 1,
3    b = 0,
4    temp
5  var seq = []
6
7  while (num > 0) {
8    temp = a
9    a = a + b
10    b = temp
11    seq.push(b)
12    num--
13  }
14
15  return seq
16}

For our training set, we’re going to generate the first 100 Fibonacci numbers:

1const fibs = fibonacci(100)

Our independent variable $X$ to be a 1D Tensor of the first 99 numbers in that sequence:

1const xs = tf.tensor1d(fibs.slice(0, fibs.length - 1))

We can obtain our $Y$ by dropping the first number in the sequence, that is the 1D Tensor that contains the values our model is going to predict:

1const ys = tf.tensor1d(fibs.slice(1))

We can take a glimpse at what our training looks like, by putting the first five values into a table:

x	y
1	1
1	2
2	3
3	5
5	8

Basically, we obtain $Y$ by shifting the $X$ values by one to the right.

Using the data as is might not produce a good model, in fact - it won’t. We’re going to apply a simple hack that will transform (scale) our data:

1const xmin = xs.min()
2const xmax = xs.max()
3const xrange = xmax.sub(xmin)
4
5function norm(x) {
6  return x.sub(xmin).div(xrange)
7}
8
9xsNorm = norm(xs)
10ysNorm = norm(ys)

Here are the first couple of $X$ and $Y$ values after applying the operation:

1X [0, 0,                     4.567816146623912e-21, 9.135632293247824e-21]
2Y [0, 4.567816146623912e-21, 9.135632293247824e-21, 1.8271264586495648e-20]

Basically, we scaled down the $X$ values in the interval [0, 1]. We almost did the same thing to $Y$ values, except we used the max and min values from the $X$ . Can you guess why?

Building our model

With our data ready to go it is time to create our model. The Simple Linear Regression is well… simple to create. Even in TensorFlow, that is. Let’s have a look at the equation describing the model once again:

Y = aX + b

First, we must initialize our model parameters $a$ and $b$ :

1const a = tf.variable(tf.scalar(Math.random()))
2const b = tf.variable(tf.scalar(Math.random()))

What the Variable wrapper does it allows the value that it holds to (surprisingly) change. The necessity for using Variable comes from the fact that we want to find better values for our parameters $a$ and $b$ and thus change them. Do you know why we initialize $a$ and $b$ with random numbers instead of 0?

Finally, it is time to write our model in TensorFlow.js:

1function predict(x) {
2  return tf.tidy(() => {
3    return a.mul(x).add(b)
4  })
5}

We’re going to skip what tf.tidy() does and discuss the important part:

1a.mul(x).add(b)

Here we just follow the formula from the above: multiply $a$ with $X$ and add $b$ to the result. I know, it is a strange syntax for such a simple thing to do, but hey you chose to learn TensorFlow.js!

Training

Roughly speaking, the training of our model consists of showing data to our model, obtaining a prediction from it, evaluating how good that prediction is and feeding back that information in the training process.

Loss function

Evaluating the goodness of the prediction is done using a loss (or error) function. We’re going to use a rather simple one - Mean Squared Error (MSE):

\text{MSE} = \frac{1}{n}\sum_{i=1}^{n}(Y_i - \hat{Y_i}) ^ 2

where $n$ is the number of $Y$ values, $Y_i$ is the $i$ -th value in $Y$ and $\hat{Y_i}$ is the prediction for $X_i$ from our model.

Roughly speaking, MSE measures the average squared difference between the predicted and real values. The result obtained from MSE is always non-negative. Results closer to 0 indicate that our model can make predictions using the provided data very well.

Here is the MSE formula from above translated into TensorFlow.js lingo:

1function loss(predictions, labels) {
2  return predictions.sub(labels).square().mean()
3}

The training loop

With the loss() and predict() functions in place you are almost ready to train your first model in TensorFlow.js. The last missing ingredient is the optimizer.

The optimizer is the workhorse behind the process of finding good parameters for your model. The main job of the optimizer is to feedback the signal from the loss function so that your model is (hopefully) continuously improved. Optimization in Machine Learning is an interesting topic that we won’t cover in this part of the series, but we will use one right now:

1const learningRate = 0.5
2const optimizer = tf.train.sgd(learningRate)

We’re using SGD optimizer with a learning rate set to $0.5$ . You can think of the learning rate parameter as a knob that says how fast our model should learn from the data presented to it. Properly setting this value is still a mystery to some, but we’re getting better at it!

The training loop itself is pretty tight:

1const numIterations = 10000
2const errors = []
3
4for (let iter = 0; iter < numIterations; iter++) {
5  optimizer.minimize(() => {
6    const predsYs = predict(xsNorm)
7    const e = loss(predsYs, ysNorm)
8    errors.push(e.dataSync())
9    return e
10  })
11}

First, we set the number of iterations for which our model will see the training data. For each iteration, the error is calculated using the predicted values. The optimizer receives the error and tries to find new parameter values which minimize the error. Additionally, we record all errors for later.

Making predictions

Did our model learn something? Let’s start by checking the first and last value in the errors list:

1console.log(errors[0])
2console.log(errors[numIterations - 1])

1Float32Array [0.29631567001342773]
2Float32Array [2.2385314901642722e-13]

Note that your values might (and probably will) vary but the last value must be pretty close

Would you look at that, initially our error was rather large, but at the end of the training process it is tiny!

Ok, let’s pick two numbers from the Fibonacci sequence and ask our model to predict the next one. Here we have them (of the top of my head):

1xTest = tf.tensor1d([2, 354224848179262000000])

Note that the second number is not in the training data.

Let’s unleash our model:

1predict(xTest).print()

1Tensor
2    [3.2360604, 573146525190143900000]

The true values are:

1[3, 573147844013817200000]

That looks alright for a simple model such as ours. Remember that our task was to learn/find good parameters for our model. The values for $a$ and $b$ found by our optimizer are:

1a.print()
2b.print()

1Tensor
21.6180301904678345
3
4Tensor
59.997466321465254e-8

Your values for $a$ and $b$ might differ, but not widely.

Looks like the important parameter is $a$ , while $b$ is pretty much useless.

Conclusion

You made it! Your first model is successfully running in the browser! It wasn’t that hard, wasn’t it? Luckily, we’re just getting started. In the next part, we’re going dive deeper in TensorFlow.js and train more complex models.

Please, ask questions or leave feedback in the comments below. Thanks!

P.S. You can find the complete source code on GitHub or have a look at it now:

1// What is a Tensor?
2
3const myFirstTensor = tf.scalar(42)
4console.log(myFirstTensor)
5myFirstTensor.print()
6
7const oneDimTensor = tf.tensor1d([1, 2, 3])
8oneDimTensor.print()
9
10// Preparing the training data
11
12function fibonacci(num) {
13  var a = 1,
14    b = 0,
15    temp
16  var seq = []
17
18  while (num > 0) {
19    temp = a
20    a = a + b
21    b = temp
22    seq.push(b)
23    num--
24  }
25
26  return seq
27}
28
29const fibs = fibonacci(100)
30
31const xs = tf.tensor1d(fibs.slice(0, fibs.length - 1))
32const ys = tf.tensor1d(fibs.slice(1))
33
34const xmin = xs.min()
35const xmax = xs.max()
36const xrange = xmax.sub(xmin)
37
38function norm(x) {
39  return x.sub(xmin).div(xrange)
40}
41
42xsNorm = norm(xs)
43ysNorm = norm(ys)
44
45// Building our model
46
47const a = tf.variable(tf.scalar(Math.random()))
48const b = tf.variable(tf.scalar(Math.random()))
49
50a.print()
51b.print()
52
53function predict(x) {
54  return tf.tidy(() => {
55    return a.mul(x).add(b)
56  })
57}
58
59// Training
60
61function loss(predictions, labels) {
62  return predictions.sub(labels).square().mean()
63}
64
65const learningRate = 0.5
66const optimizer = tf.train.sgd(learningRate)
67
68const numIterations = 10000
69const errors = []
70
71for (let iter = 0; iter < numIterations; iter++) {
72  optimizer.minimize(() => {
73    const predsYs = predict(xsNorm)
74    const e = loss(predsYs, ysNorm)
75    errors.push(e.dataSync())
76    return e
77  })
78}
79
80// Making predictions
81
82console.log(errors[0])
83console.log(errors[numIterations - 1])
84
85xTest = tf.tensor1d([2, 354224848179262000000])
86predict(xTest).print()
87
88a.print()
89b.print()

Want to be a Machine Learning expert?

Join the weekly newsletter on Data Science, Deep Learning and Machine Learning in your inbox, curated by me! Chosen by 10,000+ Machine Learning practitioners. (There might be some exclusive content, too!)

You'll never get spam from me

Hacker's Guide to Neural Networks in JavaScript

Build Machine Learning models (especially Deep Neural Networks) that you can easily integrate with existing or new web apps. Think of your ReactJs, Vue, or Angular app enhanced with the power of Machine Learning models.

Get SH*T Done with PyTorch

Learn how to solve real-world problems with Deep Learning models (NLP, Computer Vision, and Time Series). Go from prototyping to deployment with PyTorch and Python!

Hacker's Guide to Machine Learning with Python

This book brings the fundamentals of Machine Learning to you, using tools and techniques used to solve real-world problems in Computer Vision, Natural Language Processing, and Time Series analysis. The skills taught in this book will lay the foundation for you to advance your journey to Machine Learning Mastery!

Hands-On Machine Learning from Scratch

This book will guide you on your journey to deeper Machine Learning understanding by developing algorithms in Python from scratch! Learn why and when Machine learning is the right tool for the job and how to improve low performing models!