It is time to learn about value functions, the Bellman equation, and Q-learning. You will use all that knowledge to build an MDP and train your agent using Python. Ready to get that ice cream?

Here’s an example of how well-trained agents can act in their environments given the proper incentive:

Discounted Future Reward

Why do we need the discount factor $\gamma$? The total reward that your agent will receive from the current time step t to the end of the task can be defined as:

That looks ok, but let’s not forget that our environment is stochastic (the supermarket might close any time now). The discount factor allows us to value short-term reward more than long-term ones, we can use it as:

Our agent would perform great if he chooses the action that maximizes the (discounted) future reward at every step.

Value function

It would be great to know how “good” a given state $s$ is. Something to tell us: no matter the state you’re in if you transition to state $s$ your total reward will be $x$, word! If you start from $s$ and follow policy $\pi$. That would spare us from revisiting same states over and over again. The value function does this for us. It depends on the state we’re in $s$ and the policy $\pi$ your agent is following. It is given by:

There exists an optimal value function that has the highest value for all states. It is given by:

Q function

Yet, your agent can’t control what state he ends up in, directly. He can influence it by choosing some action $a$. Let’s introduce another function that accepts state and action as parameters and returns the expected total reward - the Q function (it represents the “quality” of a certain action given a state). More formally, the function $Q^{\pi}(s, a)$ gives the expected return when starting in $s$, performing $a$ and following $\pi$.

Again, we can define the optimal Q-function $Q^*(s, a)$ that gives the expected total reward for your agent when starting at $s$ and picks action $a$. That is, the optimal Q-function tells your agent how good of a choice is picking $a$ when at state $s$.

There is a relationship between the two optimal functions $V^*$ and $Q^*$. It is given by:

That is, the maximum expected total reward when starting at $s$ is the maximum of $Q^*(s, a)$ over all possible actions.

Using $Q^*(s, a)$ we can extract the optimal policy $\pi^*$ by choosing the action $a$ that gives maximum reward $Q^*(s, a)$ for state $s$. We have:

There is a nice relationship between all functions we defined so far. You now have the tools to identify states and state-action pairs as good or bad. More importantly, if you can identify $V^*$ or $Q^*$, you can build the best possible agent there is (for the current environment). But how do we use this in practice?

Learning with Q-learning

Let’s focus on a single state $s$ and action $a$. We can express $Q(s, a)$ recursively, in terms of the Q value of the next state $s'$:

This equation, known as the Bellman equation, tells us that the maximum future reward is the reward the agent received for entering the current state $s$ plus the maximum future reward for the next state $s'$. The gist of Q-learning is that we can iteratively approximate $Q^*$ using the Bellman equation described above. The Q-learning equation is given by:

where $\alpha$ is the learning rate that controls how much the difference between previous and new Q value is considered.

Can your agent learn anything using this? At first - no, the initial approximations will most likely be completely random/wrong. However, as the agent explore more and more of the environment, the approximated Q values will start to converge to $Q^*$.

Building the Environment

Okay, it is time to get your ice cream. Let’s try a simple case first:

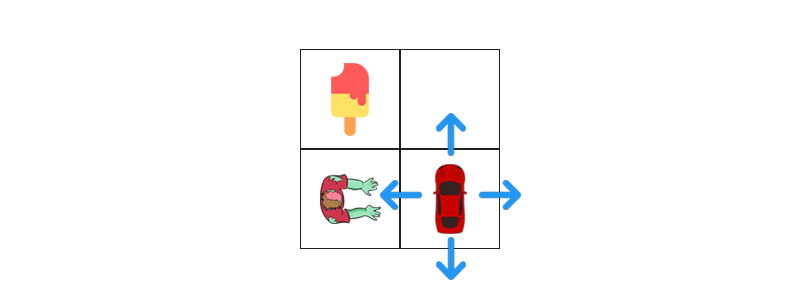
The initial state looks like this:

1ZOMBIE = "z"
2CAR = "c"
3ICE_CREAM = "i"
4EMPTY = "*"
5
6grid = [
7    [ICE_CREAM, EMPTY],
8    [ZOMBIE, CAR]
9]
10
11for row in grid:
12    print(' '.join(row))

1i *
2    z c

We will wrap our environment state in a class that holds the current grid and car position. Having a constant-time access to the car position on each step will help us simplify our code:

1class State:
2
3    def __init__(self, grid, car_pos):
4        self.grid = grid
5        self.car_pos = car_pos
6
7    def __eq__(self, other):
8        return isinstance(other, State) and self.grid == other.grid and self.car_pos == other.car_pos
9
10    def __hash__(self):
11        return hash(str(self.grid) + str(self.car_pos))
12
13    def __str__(self):
14        return f"State(grid={self.grid}, car_pos={self.car_pos})"

All possible actions:

1UP = 0
2DOWN = 1
3LEFT = 2
4RIGHT = 3
5
6ACTIONS = [UP, DOWN, LEFT, RIGHT]

and the initial state:

1start_state = State(grid=grid, car_pos=[1, 1])

Your agent needs a way to interact with the environment, that is, choose actions. Let’s define a function that takes the current state with an action and returns new state, reward and whether or not the episode has completed:

1from copy import deepcopy
2
3def act(state, action):
4
5    def new_car_pos(state, action):
6        p = deepcopy(state.car_pos)
7        if action == UP:
8            p[0] = max(0, p[0] - 1)
9        elif action == DOWN:
10            p[0] = min(len(state.grid) - 1, p[0] + 1)
11        elif action == LEFT:
12            p[1] = max(0, p[1] - 1)
13        elif action == RIGHT:
14            p[1] = min(len(state.grid[0]) - 1, p[1] + 1)
15        else:
16            raise ValueError(f"Unknown action {action}")
17        return p
18
19    p = new_car_pos(state, action)
20    grid_item = state.grid[p[0]][p[1]]
21
22    new_grid = deepcopy(state.grid)
23
24    if grid_item == ZOMBIE:
25        reward = -100
26        is_done = True
27        new_grid[p[0]][p[1]] += CAR
28    elif grid_item == ICE_CREAM:
29        reward = 1000
30        is_done = True
31        new_grid[p[0]][p[1]] += CAR
32    elif grid_item == EMPTY:
33        reward = -1
34        is_done = False
35        old = state.car_pos
36        new_grid[old[0]][old[1]] = EMPTY
37        new_grid[p[0]][p[1]] = CAR
38    elif grid_item == CAR:
39        reward = -1
40        is_done = False
41    else:
42        raise ValueError(f"Unknown grid item {grid_item}")
43
44    return State(grid=new_grid, car_pos=p), reward, is_done

In our case, one episode is starting from the initial state and crashing into a Zombie or eating the ice cream.

Learning to drive

Ok, it is time to implement the Q-learning algorithm and get the ice cream. We have a really small state space, only 4 states. This allows us to keep things simple and store the computed Q values in a table. Let’s start with some constants:

1import numpy as np
2import random
3
4random.seed(42) # for reproducibility
5
6N_STATES = 4
7N_EPISODES = 20
8
9MAX_EPISODE_STEPS = 100
10
11MIN_ALPHA = 0.02
12
13alphas = np.linspace(1.0, MIN_ALPHA, N_EPISODES)
14gamma = 1.0
15eps = 0.2
16
17q_table = dict()

We will decay the learning rate, alpha, every episode - as your agent explores more and more of the environment, he will “believe” that there is not that much left to learn. Additionally, limits for the number of training episodes and steps are defined.

Dicts in Python can be a bit clunky, so we’re using a helper function q that gives the Q value for a state-action pair or for all actions, given a state:

1def q(state, action=None):
2
3    if state not in q_table:
4        q_table[state] = np.zeros(len(ACTIONS))
5
6    if action is None:
7        return q_table[state]
8
9    return q_table[state][action]

Choosing an action given the current state is really simple - act with random action with some small probability or the best action seen so far (using our q_table):

1def choose_action(state):
2    if random.uniform(0, 1) < eps:
3        return random.choice(ACTIONS)
4    else:
5        return np.argmax(q(state))

Why your agent uses random actions, sometimes? Remember, the environment is unknown, so it has to be explored in some way - your agent will do so using the power of randomness.

Up next, training your agent using the Q-learning algorithm:

1for e in range(N_EPISODES):
2
3    state = start_state
4    total_reward = 0
5    alpha = alphas[e]
6
7    for _ in range(MAX_EPISODE_STEPS):
8        action = choose_action(state)
9        next_state, reward, done = act(state, action)
10        total_reward += reward
11
12        q(state)[action] = q(state, action) + \
13                alpha * (reward + gamma *  np.max(q(next_state)) - q(state, action))
14        state = next_state
15        if done:
16            break
17    print(f"Episode {e + 1}: total reward -> {total_reward}")

1Episode 1: total reward -> 999
2    Episode 2: total reward -> 998
3    Episode 3: total reward -> 997
4    Episode 4: total reward -> 997
5    Episode 5: total reward -> 999
6    Episode 6: total reward -> 999
7    Episode 7: total reward -> 998
8    Episode 8: total reward -> -100
9    Episode 9: total reward -> -101
10    Episode 10: total reward -> 999
11    Episode 11: total reward -> 999
12    Episode 12: total reward -> 999
13    Episode 13: total reward -> 999
14    Episode 14: total reward -> 999
15    Episode 15: total reward -> 999
16    Episode 16: total reward -> 998
17    Episode 17: total reward -> 999
18    Episode 18: total reward -> 999
19    Episode 19: total reward -> 999
20    Episode 20: total reward -> 999

Here, we use all of the helper functions defined above to ultimately train your agent to behave (hopefully) kinda optimal. We start with the initial state, at every episode, choose an action, receive reward and update our Q values. Note that the implementation looks similar to the formula for Q-learning, discussed above.

You can clearly observe that the agent learns how to obtain a higher reward, really quickly. Our MDP is really small, though, and this might be just a fluke. Moreover, looking at some episodes, you can see that the agent hit a Zombie (twice).

Did it learn something?

Let’s extract the policy your agent has learned by selecting the action with maximum Q value at each step, we will do that manually, like a boss. First up, the start_state:

1sa = q(start_state)
2print(f"up={sa[UP]}, down={sa[DOWN]}, left={sa[LEFT]}, right={sa[RIGHT]}")

1up=998.99, down=225.12, left=-85.10, right=586.19

UP seems to have the highest Q value, let’s take that action:

1new_state, reward, done = act(start_state, UP)

The new state looks like this:

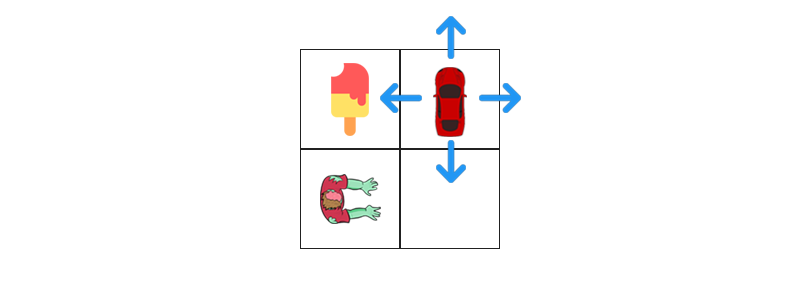
What is the best thing to do now?

1sa = q(new_state)
2print(f"up={sa[UP]}, down={sa[DOWN]}, left={sa[LEFT]}, right={sa[RIGHT]}")

1up=895.94, down=842.87, left=1000.0, right=967.10

But of course, going left will get you the ice cream! Hooray! Your agent seems to know it’s way around here.

Isn’t this amazing? Your agent doesn’t know anything about the “rules of the game”, yet it manages to learn that Zombies are bad and ice cream is great! Also, it tries to reach the ice cream as quickly as possible. The reward seems to the ultimate signal that drives the learning process.

We’re done here! You can now build complex agents that find optimal policies quickly. Except, maybe not. This was a very simple MDP. Next, we will find how Neural Networks fit into the Reinforcement Learning framework.